Reflecting on a New Course
- Matt Felton-Koestler
- Apr 27, 2019
- 4 min read

This semester I was able to teach a new course focused on middle grades (4-9) math teaching for future middle grades and secondary (grades 7-12) teachers. I think it has been one of my favorite classes since coming to OU. Before creating this new course, middle grades teacher candidates only took one math methods course, so now they will have two. I'm using this new first class, which does not include a placement in a classroom, to focus on expanding perspectives about what counts as mathematics and to build up a familiarity with a focus on problem solving, real-world connections/math modeling, and justice. That way, when they get to the next methods course, which does include a classroom placement, they have a foundation to work from when I ask them to teach lessons out in the field.
Lesson Portfolios
One thing we did that I think was pretty successful was develop a portfolio of lessons. For almost every activity we did in class I wrote up a brief summary of the activity. Then they had to add information about the math content and practices, possible modifications they would make if they were to use it, and reflect on their experience with it.
These were also supplemented by: (1) Lesson plans the found from high quality resources like NCTM articles or YouCubed, and (2) Ideas for possible connections to social or political issues they found in the news.
My intent is that they will use these in the next methods course and in their future careers.
End of Semester Reflection: Concept Maps
To reflect at the end of the semester we used concept maps, which I haven't used before. Something I have done before is to give out cards with descriptions/reminders of activities we did in class and ask groups to come up with some way of sorting them. But I was looking to try something new, in part because I thought this was a little limiting in that it made the focus a bit to narrow and tended to lead to basically a Venn diagram of tasks/activities.
Below is a slide show of the slides I used as prompts. These were the only directions I used. I had the slides on one screen and then a timer on the other screen to keep us on track for each section.
I started with the following short video to introduce concept maps (slide 1). I didn't know what my students knew about them and I thought it was good to give a quick overview and some examples of what they might look like:
I then included a range of example images I found here to try to encourage multiple representations (slides 2-4), although I did mention that I thought most of ours would look more like the last one.
Then I made sure they brainstormed on their own for awhile to get their own ideas in place (slide 5).
Next (slide 6), I gave everyone a copy of a list of activities from our class and briefly reviewed it verbally. This was to help jog their memories and push them to consider the breadth of activities we did during the semester. I then gave them a few more minutes to work individually (slide 7).
The bulk of the time was spent on them working as a group to develop their concept maps (slide 8)--each table had a large piece of chart paper in the middle of the table and a box of markers. I think it is worth noting that they have been in these groups all semester. I didn't assign seats, but they consistently sat in them and virtually everything we do in class involves group work or collaboration. They were reshuffled for a couple of days for one lesson, but after that they returned to these groups.
We ended with a gallery walk, with some explicit directions to push them to interact, and a whole class discussion (slides 9-10).
Their Concept Maps
I was pretty pleased with what they came up with! For the record, on the course syllabus I wrote the following (I never feel like I accomplish everything I aim to):
This course will focus on developing the tools and dispositions you need to continually improve your mathematics teaching. In this course you will learn to:
solve mathematics problems in multiple ways;
represent important mathematical concepts in multiple ways;
anticipate common children’s strategies and analyze their thinking;
create and teach lessons that
connect to mathematics learning standards,
use research-based teaching methods, and
make mathematics accessible and challenging to a broad range of learners; and
make connections between math and other disciplines, students’ lives, and the real world.
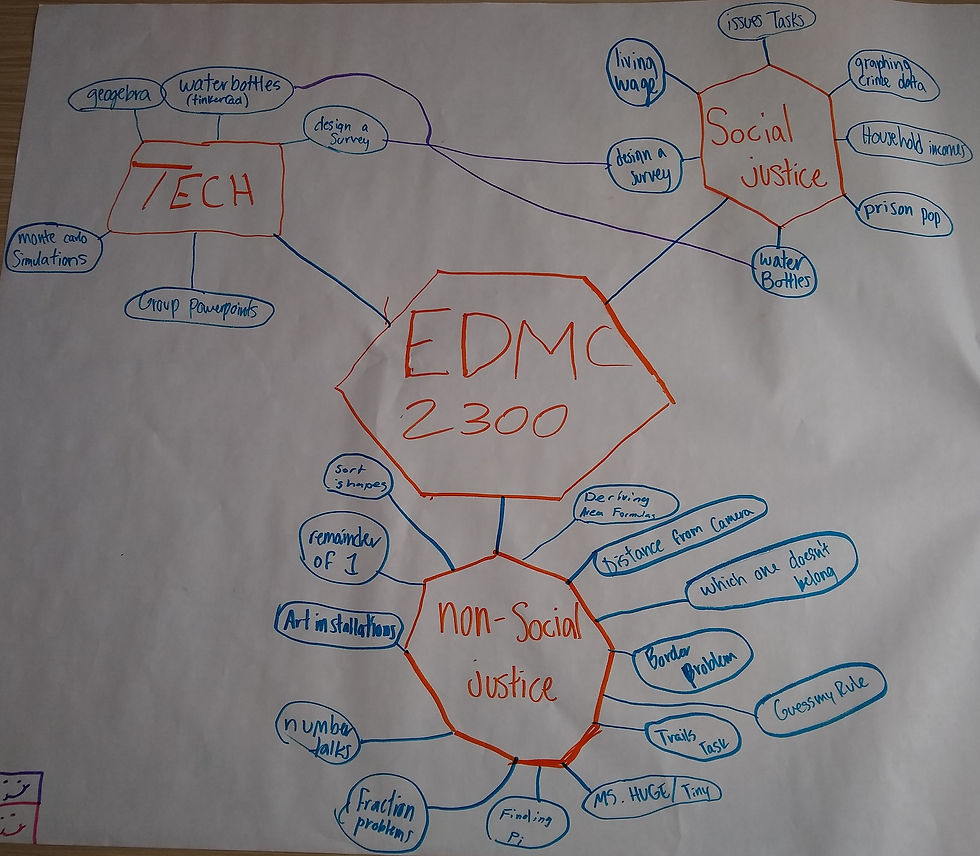
I liked the nonagon of non-justice.
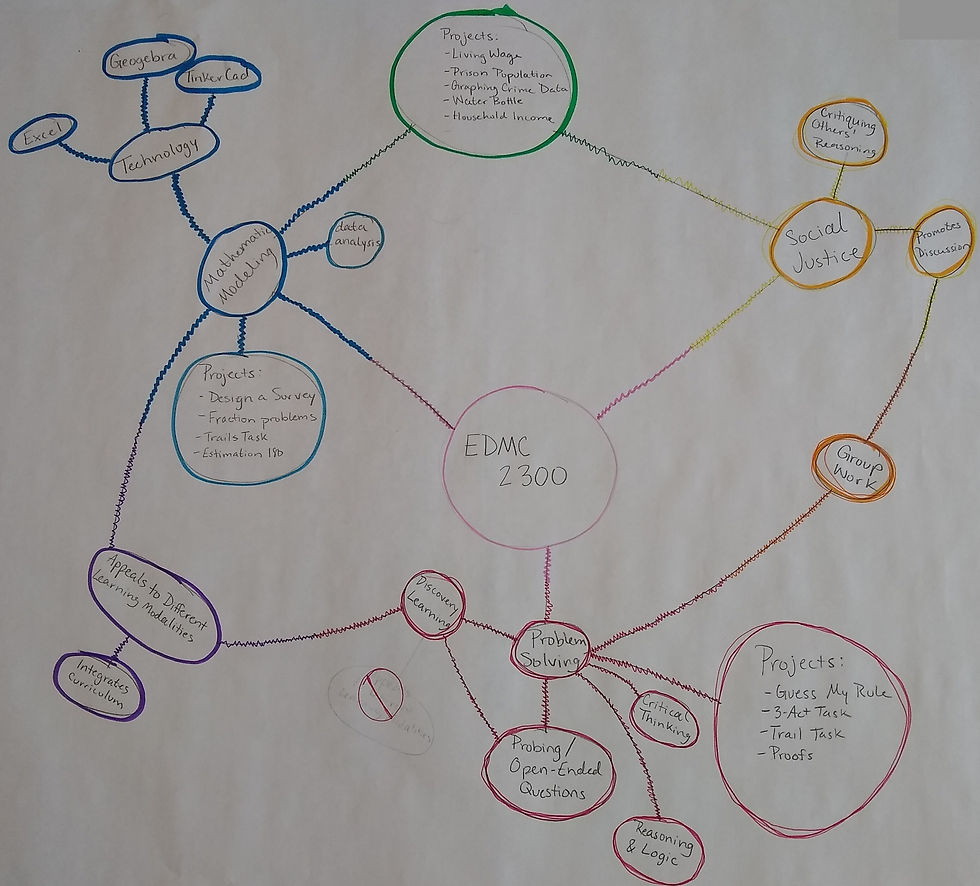
It's a little hard to see their coloring, but ideas that are in-between other colors are a blend of those two colors (e.g., the green is a mixing of blue and yellow).
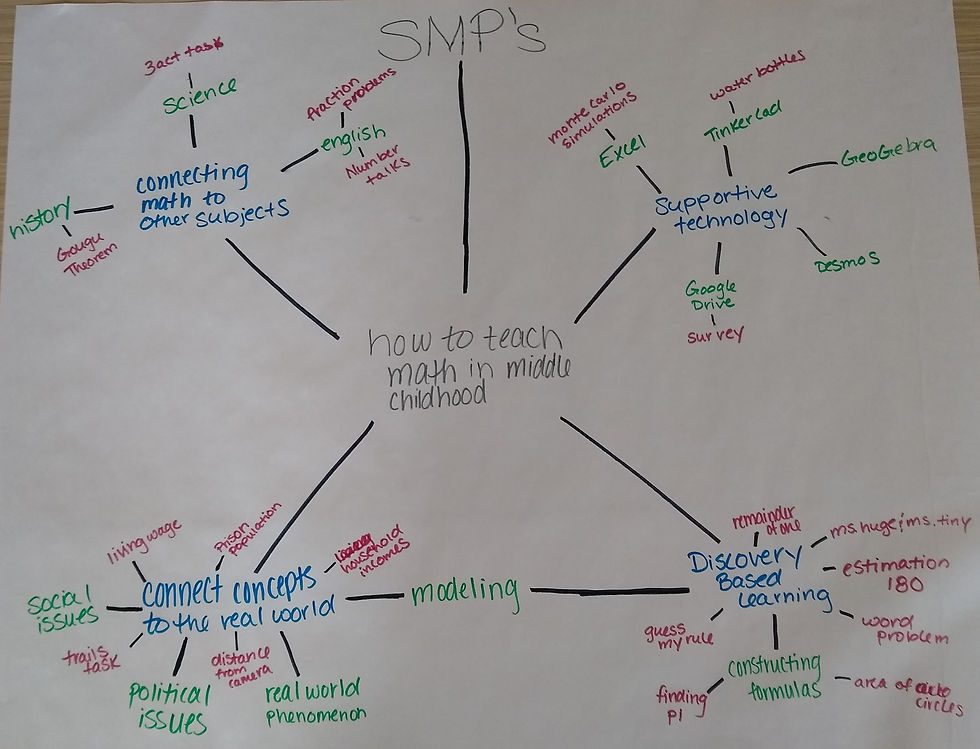
"How to teach math in middle childhood" was their central concept, but the standards for mathematical practice (SMPs) informed almost everything we did in class, which is why they are at the top leading into their central concept.

The dashed lines represent connections.

Big ideas are in pink, sub-ideas are in green, and specific class activities are in orange.

There's a lightening bolt because they were brainstorming. This group organized theirs around the actions a teacher takes: (1) planning, (2) enacting in the classroom, and (3) reflecting on how it went.
Short URL: http://bit.ly/MatWConceptMaps





















Comments