This morning, over his morning oatmeal, I asked Parker to think about a classic math task. I began with a single hexagon with the dots around it. Below is an abridged version of our conversation.
A lot of times people look at child-centered mathematics (the kind of math I describe in this blog, and that is advocated by math ed researchers and professional organizations) and say the teacher isn't doing any teaching. In fact, the teacher is extremely active in thinking about what kinds of questions to pose and how to pose them.
What Parker is able to do with me, one-on-one, is obviously different than how it would go when trying to work with a whole class--but the idea that the teacher is actively working to figure out kids' thinking and then posing appropriate follow up tasks (say the next day) or questions (in the moment) is central to child-centered thinking. In the exchange below I make a number of decisions about what questions to pose based on my evolving understanding of Parker's evolving understanding. Teachers are more active in child-centered classrooms--they are just active in different ways.
M: Pretend this is a table, how many people can sit here?
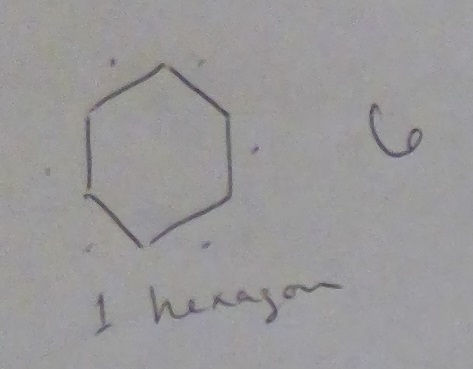
P: 6
M: [So I drew two hexagons] Now how many people?
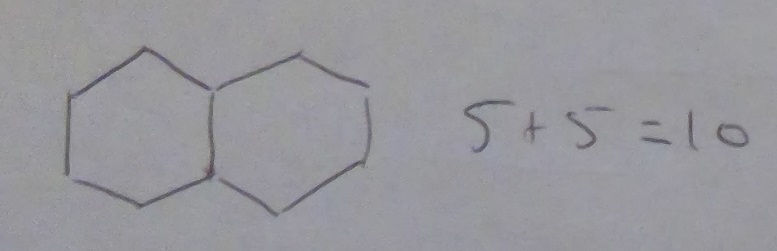
P: 10. When you put two tables together one of the sides is covered by the other table and vice versa. So I did 5 and 5.
M: [I write "5 + 5 = 10" and draw three hexagons]
P: 15. No, no, don't use that answer. At first I thought 15, but the middle table has two sides blocked off. 5 + 5 = 10. 14.
M: [I notate his work and draw 6 hexagons]. I can help you add up the numbers if you tell me what numbers to add. [My goal is to focus on the underlying rule/process, not the calculations.]
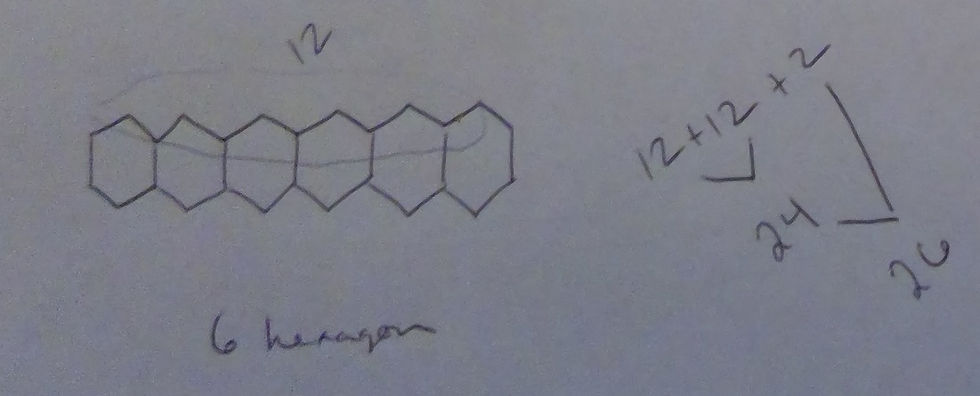
P: [After thinking for a bit] I'm going to use a new strategy. [He counts along the top by twos, touching each top-point as he counts] 2, 4, 6, 8, 10, 12. 12 on top, 12 on the bottom, and 2 more.
M: [I notate his work and draw "10" hexagons (this later got changed to 100). I drew them "generically" so he couldn't count them.] How many if there are 10 hexagons? I drew it funny so you have to use some of your imagination.
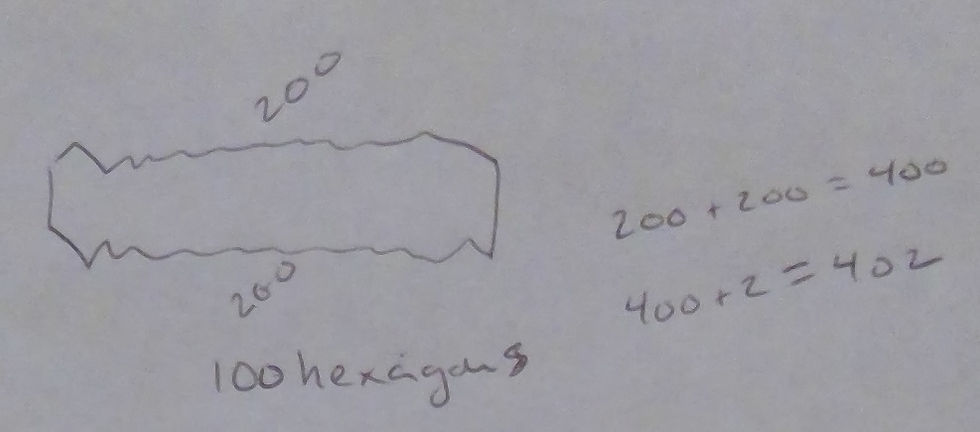
He was stuck here. He tried to use the 6 hexagon image and count on by twos from there, but he couldn't keep track of everything in his head and on his fingers.
M: There's a lot to keep track of, huh. Let's try your strategy with the one with 3 hexagons. How would it work?
We went through the strategy for 3, 2, and 1 hexagon.
M: [I go back to the "10" hexagon image, but change it to 100. I choose 100 because (a) it will take forever to count by two's, but (b) it's an easy number for him to double if he recognizes the relationship.] What if there were 100 hexagons? How many seats would there be on the top?
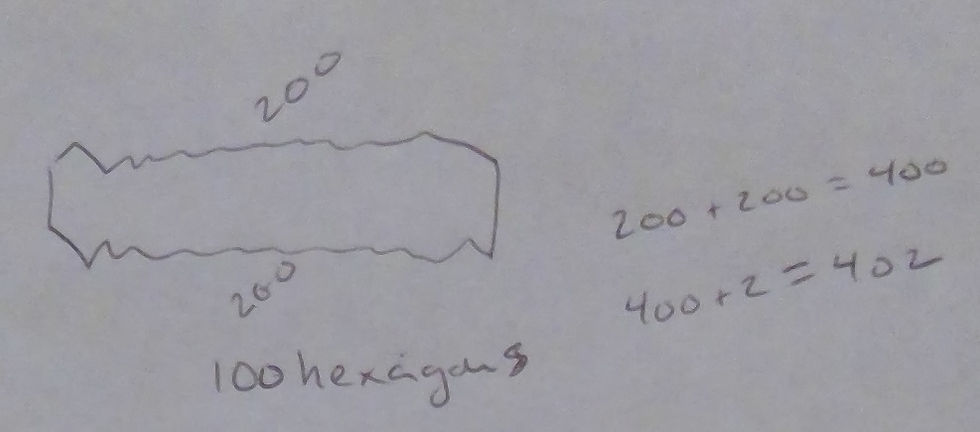
P: 200
M: So how many seats altogether?
P: 200 plus 200 is 400.
M: Done?
P: No, and 2 more. 402.
M: Done?
P: Yeah.
M: [I notate his work.] Okay, one more. What if there were 328 hexagons? I will do all the calculations if you do all the math thinking.
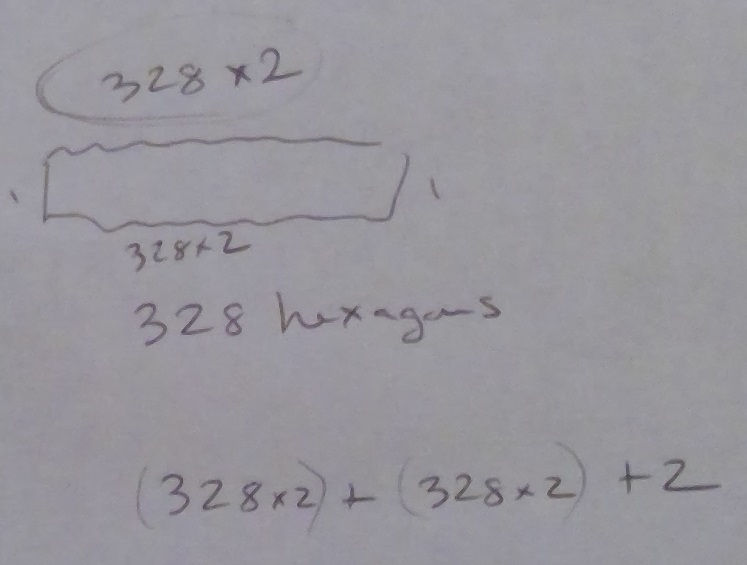
P: It would be double 328 on the top.
M: Do you know a way to say double with math symbols?
P: No
M: Like could we use plus or times to show it?
P: We could use times!
M: How would I write it?
P: 328 times 2.
M: I was also thinking 328 plus 328.
P: I think this way [times] is a little better.
M: Okay, so how many on the bottom?
P: The same thing.
M: So what would our whole number sentence look like?
P: ...
M: [I circle the top "328 x 2"] We can just write this even if we don't figure out what it is.
P: 328 times 2, plus 328 times 2, plus 2.
Short URL: http://bit.ly/2N6RP5F
Leave a Comment
Post a comment below, on my Facebook post, or on my Tweet.