Summer Math: Context Matters
- Matt Felton-Koestler
- Jul 31, 2018
- 4 min read

We recently visited Bay Beach Amusement Park while in Wisconsin (it's awesome by the way). Rides there cost between 1-4 tickets and tickets cost 25 cents a piece. Before going we debated how many tickets to buy and ended up deciding to spend $20 to start. Before getting in the car I asked Parker how many tickets that would be. He said he wanted paper to work on and so we got his journal for him to work in the car.
Each dollar gives you 4 tickets, so I see this problem as 20 groups of 4, or 20 × 4. For me (as a mathematically fluent adult) 20 × 4 = 4 × 20. They (20×4 and 4×20) are "so equal" in my mind that they are basically the same—I don't even think about it. The problem just becomes "4 twenties", which is 80. (I'm convinced that the only reason I see any difference between 20×4 and 4×20 is because I'm a math educator who spends time thinking about that type of thing.)
But for children there's often a difference between these two situations:
20 groups of 4 (often written as 20×4). For instance: "I have 20 dollars and each dollar buys me 4 tickets."
4 groups of 20 (often written as 4×20). For instance: "I have 4 strips of tickets and each strip has 20 tickets in it."
Mathematically they are equivalent, and in fact one of the powerful features of mathematics is that I can change 20×4 into 4×20 to make my life easier, even if it doesn't perfectly map onto the situation I'm dealing with.
Based on past things I have done with Parker I think he could quickly figure out that 4 groups of 20 was 80 in his head and/or with his fingers. But Parker didn't approach this problem as 4 groups of 20. He approached it in a way that matches the context: as 20 groups of 4. So he got out his journal and started adding 4's.
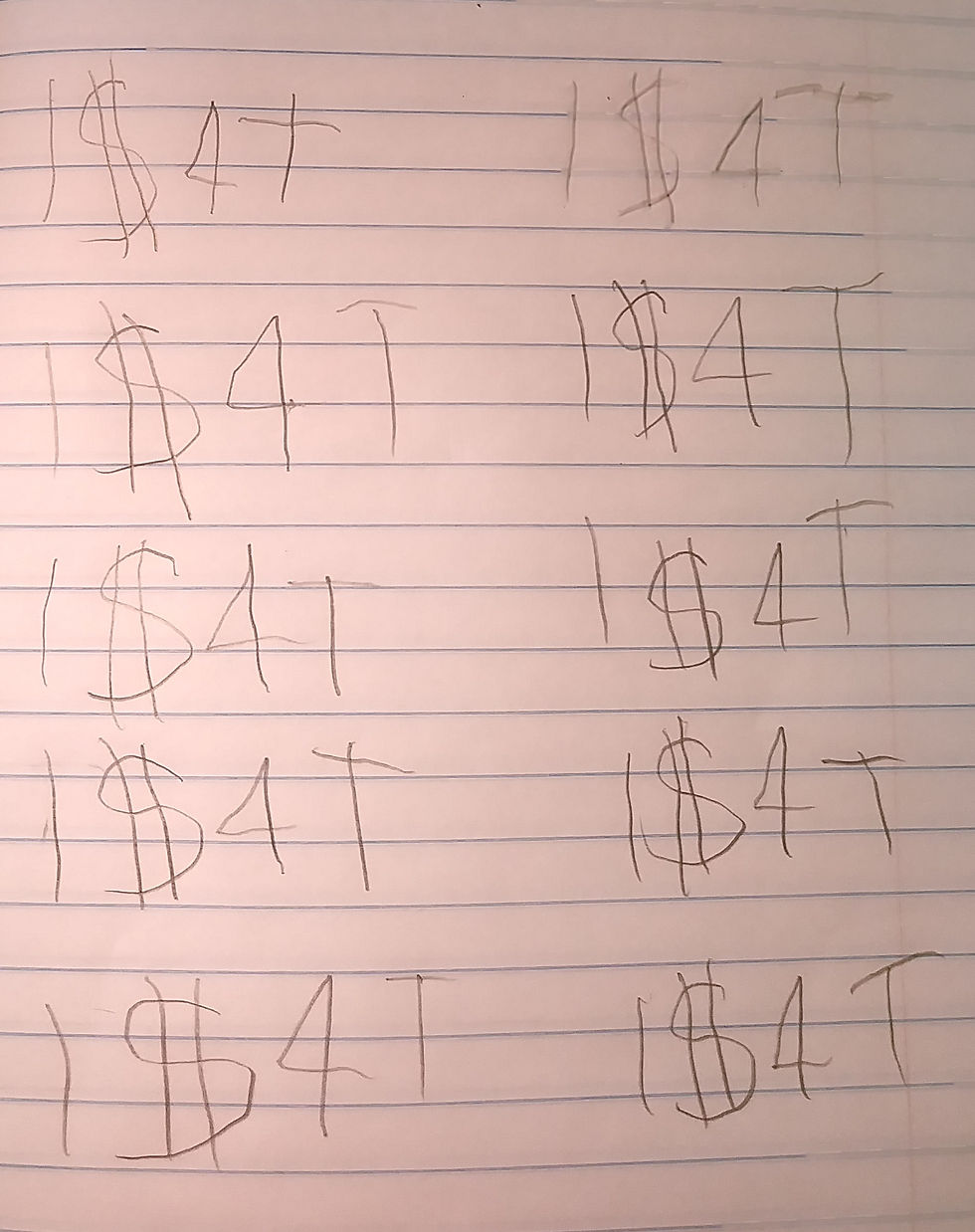
Adding 4 twenty times is much more laborious than adding 20 four times. But his strategy matches the problem context. And using a strategy that matches the context is very common when children are allowed to develop their own strategies. Children have a natural tendency to make meaningful connections between the real-world context and the mathematics they are doing. Unfortunately, in school they are often pushed to use abstract strategies that are disconnected from the context. What they learn is that the context doesn't matter and that math is not connected to the real world.
Imagine a classroom where students are taught to: (1) Identify the type of problem they are dealing with. Maybe they are even taught to look for "key words" like "each" as an indicator of multiplication (key words should never be taught—they don't work for all problems and they teach kids to turn off their thinking). (2) To write an equation that goes with this situation, like "20 × 4 = ?" (3) To calculate the answer to this equation—likely using memorized facts like flipping the numbers (to 4×20) and/or the times table.
In some respects this is more "efficient." It roughly matches my own adult thinking. I solved the problem in no time, so you might ask, "shouldn't we teach kids to do this?"
The problem is it turns off the child's sense-making. It's much more valuable to invest time in ensuring that math is a meaningful activity and to build meaning for mathematical symbols out of contexts that children understand. Otherwise math becomes a meaningless activity of "guess the rule to use", which is why so many children end up getting lost in math by upper elementary or middle school.
Pushing Kids Along
Of course, we cannot wait forever. Children are not going to naturally reinvent all of mathematics on their own in grade school. But the method of pushing them along should be through carefully selected problems, not by forcing them to memorize rules or use abstract strategies.
In this case, I might wait and see if after a few problems like this any kids naturally flipped the numbers. In many cases some kids will do this. If this happened it would provide an opportunity for a discussion about why that works and whether it works in other cases.
Alternatively I might create problems that are more likely to spur this kind of thinking. I could have problems about cookies on a cookie sheet or tiles on a bathroom floor and ask kids to draw pictures to represent the situation. These problems have a structure that makes them more likely to be tackled in more than one direction (as 20×4 or as 4×20) because the "groups" aren't as obvious (rows make just as good a group as columns do). Or, to stick with the ticket theme, I could claim there was a ticket dispenser and they came out as a big sheet of perforated tickets that was four tickets wide. The sheet would be longer or shorter depending on how much you paid (so in this case it would be 4 tickets wide and 20 tickets long).
Finally, I can always say something like "I saw a kid in another class do it this way... Does that work? Would it work for other numbers?"
What these approaches have in common is that they pose the new strategy as a problem to be explored, as an open question. They also require the students to make sense of how and why flipping the numbers makes sense and how they can be connected to the context. In other words, they keep sense-making and a meaningful connection to the real world at the center of the conversation.
Short URL: http://bit.ly/2LDQC5U
Leave a Comment
Post a comment below, on my Facebook post, or on my Tweet.

Comments