Ours is not to reason why…
- Matt Felton-Koestler
- Sep 19, 2017
- 5 min read
…just invert and multiply!
This post is a bit longer and a bit more didactic than many of my others, but I think it's interesting all the same, and it's certainly important information for future teachers (like my students!).
I'm guessing that many of you learned the following algorithm for dividing fractions:
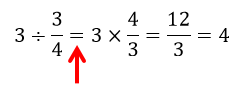
It's this first step (the one marked with the red arrow), where dividing by 3 fourths turns into multiplying by 4 thirds, that I'm going to talk about today. But to do that I need to go back to early approaches to teaching multiplication and division.
A Story of Groups
In the elementary grades multiplication and division are most commonly introduced with situations like the following:
I have 3 bags. Each bag holds 4 marbles. How many marbles do I have?
I have 12 marbles. I have 3 bags that I want to put my marbles in. How many marbles will each bag have if I split them up equally?
I have 12 marbles. I want to put 4 marbles in each bag. How many bags do I need?
These are all variations on the following situation:
I have 3 bags. I can fit 4 marbles per bag. I have 12 marbles.
3 bags × 4 marbles per bag = 12 marbles
All that changes is the unknown:
3 bags × 4 marbles per bag = ? marbles
3 bags × ? marbles per bag = 12 marbles
? bags × 4 marbles per bag = 12 marbles
More generally, the situation is:
A groups × B amount per group = C amount
For amount per group unknown problems, children will often get out 12 blocks and deal them out one at a time (or more haphazardly) into 3 different piles. Their answer will be how many blocks end up in each pile.
For number of groups unknown problems, children will often get out 12 blocks and remove groups of 3 at a time. Their answer will be how many groups they were able to make.
Equal groups situations like these are not the only ways to think about multiplication and division, and it can be limiting if that's all the children are exposed to. However, they are the primary way in which multiplication and division are introduced in the early grades.
Extending to Fractions
Okay, so how do we extend to fractions? A lot of the equal groups story problems don't extend well to fractions. You can fill a bag half way up, but you can't really have a fraction of a marble. However, the basic structure of the problems above can still be used to pose problems about fractions.
A groups × B amount per group = C amount
? days × 3 fourths mile per day = 3 miles
Some workers need to pave 3 miles of road. They can pave 3 fourths of a mile per day. How many days will it take them?
I encourage you to try solving this problem with a picture. A number line, or a long rectangle representing three miles might help. DO NOT try to invert and multiply on this problem. It will work, but it's not at all useful in understanding what's happening. In fact, by solving this problem we're going to discover an entirely different algorithm for dividing fractions. Scroll down to see my solution.
...keep scrolling...
...almost there...
Bouya! Check this strategy out:

Let's talk about what happened here symbolically:
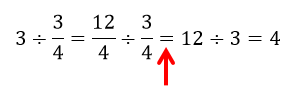
That second to last step (the one marked with the red arrow) is a little miracle. Think about the problem. Instead of thinking about 3 miles, I thought about 12 fourth-miles. And I know I need groups of 3 fourth-miles. Basically, I turned the problem into:
The workers have 12 pieces of road to pave. They can pave 3 pieces per day. How many days will it take them?
I turned it into a whole number division problem. This is called the common denominators algorithm for dividing fractions. And it always works. Not to freak you out, but in general:

Go ahead, try it out with any two fractions. I'm willing to bet that many of you had no idea there was another algorithm out there for dividing fractions!!!
What About Invert and Multiply!?
If you were to ask most people what 3 divided by 3 fourths means, they would probably say something like "it's how many times 3 fourths fits into 3." This is basically equivalent to the story problem above—it's asking how many groups of 3 fourths there are in 3. This (the number of groups unknown) is also the approach that shows up in most textbooks and classrooms.
But there's that other type of division. The amount per group unknown type. Let's look at one of those problems:
A groups × B amount per group = C amount
3 fourths of a bucket × ? gallons per bucket = 6 gallons
You pour 6 gallons of water into a bucket. The bucket is 3 fourths full. How much water does the whole bucket hold? (i.e., how many gallons per bucket?)
First, it's worth asking yourself "does this feel like division?" It's the same situation we saw back in the early introduction of division with whole numbers (amount per group unknown), but it doesn't feel like division to a lot of people. However, it can be solved using division. It's worth observing that this type of fraction division problem is relatively rare in many U.S. classrooms.
I encourage you to solve this problem using a picture. Starting with a picture of a bucket might help. Scroll down to see my solution.
...keep scrolling...
...almost there....
Bouya! Check this strategy out:
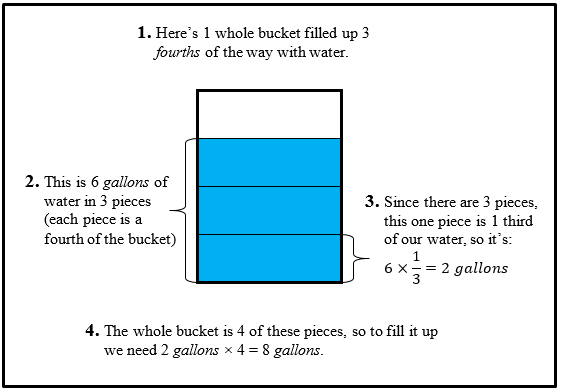
Let's talk about what happened here symbolically:
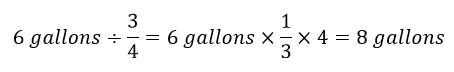
I had 6 gallons. That 6 gallons was the same as 3 pieces, so I took 1 third of my 6 gallons. But I needed 4 pieces to make a whole bucket, so I multiplied it by 4.
You know what that looks like:
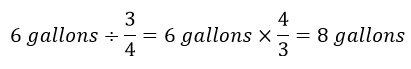
There are other ways to explain why the invert and multiply algorithm makes sense, but if you are going to pose story problems about fractions, it's worth noting that this story problem type (amount per group unknown) provides a better foundation for understanding the invert and multiply algorithm, while the most commonly used type of problem in U.S. classrooms (number of groups unknown) provides a better foundation for the common denominators algorithm (which is rarely taught).
Post a Comment
What do you remember about learning to divide fractions? Does the bucket problem feel like division to you? Did you know about the common denominators algorithm?


Comments