Watching Middle School Number Talks
- Matt Felton-Koestler
- Sep 15, 2017
- 5 min read
This post brings together number talks, doing fractions, and ways to work on math with your child without doing drills.
Recently, Courtney asked me to give her advice on which of two videos of number talks to use with a group of teachers. Parker was there, so we watched them together. In the video the kids do a series of related division problems, starting with whole numbers and moving into fractions. This video is from Sherry Parrish's Rational Number Number Talks book. It might help to watch the whole clip before reading on.
Doing the Number Talk with Parker
Parker and I would watch a bit of the video, and then pause it to discuss his thinking.
Parker's Thinking on 6 ÷ 3
The first problem in the video is 6 ÷ 3, which serves more as a support/point of connection for the students to work from on the fraction problems. This is more advanced than what Parker is capable of thinking about, but the series of problems is designed to emphasize proportional reasoning by using the idea that each pair of numbers is half of the previous pair. In other words, because you cut the 6 and the 3 in half, the ratio between the two new numbers should be the same (it's still 2). At around 2:10 Natalie uses this strategy in the video.
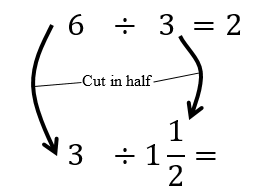
Anyway, back to Parker's thinking.
M: Do you see what it says on the board there, "6 divided by 3"?
P: What does 6 divided by 3 mean?
M: Do you want me to tell you with a story problem or with numbers?
P: Tell me with numbers
M: Division can mean at least two different things. The way that I think will be helpful for you watching this video is that it's like saying how many times does 3 fit into 6?
P: Oh easy, 2
M: How do you know that?
P: 3 and 3 is 6 and it's just like another way to say that. What's the other way? [the other thing division can mean]
M: You have 6 things and you're going to split it up into 3 groups. How many does each group get?
P: 2
M: How do you know that?
P: 2 and 2 is 4 and 2 more is 6
Parker's Thinking on 3 ÷ 1½
At around 30 seconds in the teacher poses the second problem: 3 ÷ 1½
M: Don't worry about how they wrote it. That says "1 and a half." So the problem is "3 divided by 1 and a half."
P: That's 2.
M: How did you get that?
P: The 1 and 1 is 2. A half and a half is 1. And 2 and 1 is 3.
Basically Parker is explaining how he can add 1½ and 1½ to get 3, so therefore two "1 and a half"s fit into 3.
Parker's Response to a Jamier's Strategy
At around 1:20 in the video Jamier shares his thinking: "1 times 2 equals 2 and then 1 half times 2 equals 1, so you add em up and that's 3."
M: What do you think about his strategy?
P: Yeah
M: Why?
P: Because what I heard was he had the same strategy as me
M: But he said times, you didn't use any times
P: ... They just did the same thing. The same exact strategy, but they didn't use the same numbers and words as me. But from what I heard from that times and stuff it seems like my strategy.
Parker's Thinking on 1½ ÷ ¾
At around 3:50 in the video the teacher poses the last problem: 1½ ÷ ¾
M: Okay, that says "1 and a half divided by three fourths"
P: I don't get that
M: Do you want a story or do you want to just not do it?
P: A story. Do you remember that gallon story? I want you to remember how we did that and then do it like that.
M: It's actually a lot like the gallon story. So, you're going on a hike. Every day you drink three fourths of a jug of water. You have 1 and a half jugs of water. How many days can you hike? So you have...
P: Just don't say it... You can hike 2 days.
M: How did you get that?
P: What I said was. You have the. We have the one jug of water. Let's just drink three of it. We have that part of it covered. You still have one more. You still have a half and that... Wait that can't be right. I thought you had two halves... part of my body says you can survive two days. One part says you can survive one day.
M: How do you want to find it out? Draw a picture?
So Parker drew the picture below. He has two large rectangles for the two gallons of water. He split each gallon into fourths. Then he took three of them (on the left), and grouped them together, writing a "3" for the three fourths needed. Then he took the one fourth left over and the two fourths on the right (the "half" gallon from the problem) to make another three fourths.
P: Wait, yeah, that's one, two, three, so yeah you can survive two days?
M: How come? How'd you figure it out?
P: For this one you might be a little confused. I put the last two fourths on the top so it wasn't full.

M: Awesome. That's a good strategy. I don't think you could have done it without a story.
P: When I came up with the gallon idea... I found
M: If you can't do a problem with just numbers, making a story for it can help you solve it.
The Importance of Story Problems
This last point, about story problems, is extremely important. Most kids and teachers find fractions daunting. In fact, my middle childhood students (who are preparing to become teachers) often tell me they don't think the kids in their classrooms are going to be able to do the fraction problems I assign because they are still working on things like multiplication or division. But many young kids (like kindergartners and first graders) can solve problems about fractions when they are posed in a story. Children have a strong ability to imagine and act out simple stories (with a drawing or tools). The book Extending Children's Mathematics is an excellent resource for learning to use children's natural problem-solving abilities.
In general, new mathematics should be introduced through a context that is real or realish. It doesn't have to be a real life dilemma, but it should be a context that students can imagine and can manipulate by playing out the scenario in their head, with a picture, or with physical manipulatives. Carefully selected story problems (like the one here) are one approach, but more "abstract" contexts can work too (as the S-Pattern Task) if it's something the learner is able to work with.
Speaking even more generally, children best learn math (and other) concepts by having opportunities to think about the concept before being introduced to formal notation. Even for "6 divided by 3" I had to explain what that meant (how many 3's go into 6) before Parker could engage with it. Later, we can use more formal language or notation as a label for children's thinking. This way new vocabulary, notation, etc. can be connected to their current understandings.
Send Me a Message!
What are your experiences with fractions and story problems? Have you done number talks like these with your students?


Comments