Try to Get Lower
- Matt Felton-Koestler
- Sep 1, 2017
- 5 min read
On Meet the Teacher night before the school year started we got a little bag of math mainpulatives to take home. It says we need to keep them handy so we have them available to use throughout the year. The bag has 20 transparent discs/counters (10 yellow and 10 red). It also has two 10-sided dice (1 yellow and 1 red) and two 6-sided dice (1 yellow and 1 red).
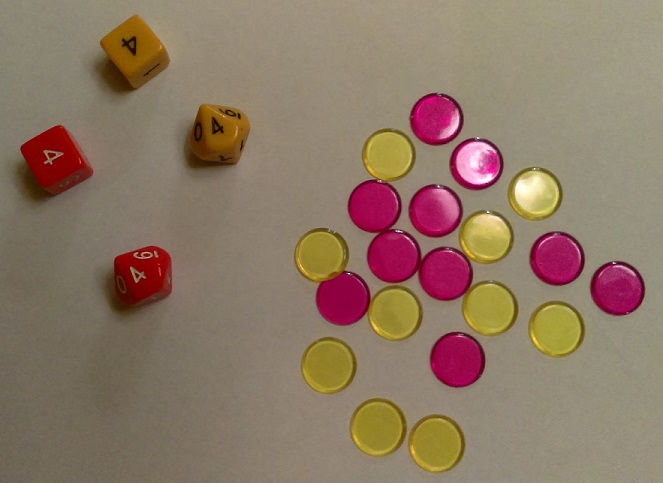
Parker was messing around with them and invented the following game (these are the rules as I now understand them—as you'll see below I didn't understand them at first):
You roll a die
You close your eyes and then take that many discs from the middle
If you have more of your color, you get -1 points
If you have more of the other color, you get +1 points
If you have the same of each color, you get 0 points
You return the discs to the middle
We played a few rounds and kept a running total of our scores. Parker was going into the negative and I could see he was a bit bummed. I was excited about doing stuff with negative numbers, so I told him that in some games, like golf, you want a low score, and he came up with the name Try to Get Lower.
A Different Game
Initially we kept getting things like 5 reds and 4 yellows, so I misinterpreted the rules at first. I thought it worked like this: Let's say you were red (and remember your own color is negative) and you got 5 reds and 1 yellow, then you would get -4 points (because -5 and 1 makes -4). But according to Parker's rules it was still just -1 points. For Parker it was just about whether you get more or less of your color.
I showed Parker what I meant by having my 1 yellow cancel 1 of my reds, leaving me with 4 more reds to make -4. Parker got the idea and we played a couple rounds like this and tried to keep track of the score. Note: This approach of canceling out different colored discs is one way of teaching negative numbers in child-centered middle grades curricula.

What's Lower/Smaller?
At one point Parker had 2 points and then got -4. It took him a couple times of me asking "how did you get that?" to figure out his new score would be -2. We ended there (it was getting late and Parker was quickly becoming far more interested in flipping over his seat cushion than in figuring out the score). I had a score of 0 and I asked who was lower... Things got a little rocky at this point. Parker agreed that with temperature -2 was lower than 0, but he said that with numbers it didn't work that way. This is a common way of thinking when children learn about negatives. -2 just doesn't feel smaller than 0. I mean 0 is nothing, right?
And this is the crux of the issue, notice that in the paragraph above sometimes I said "lower" and other times I said "smaller." When we're dealing with positive numbers, lower, less than, and smaller are all pretty interchangeable (as are higher, greater than, and bigger). But once we add negatives into the mix smaller and bigger take on a different meaning. We tend to associate them with size (or magnitude). The absolute value of -4 (written |-4|) is the same as the absolute value of 4... it's "4." Both 4 and -4 are four away from 0.
On the other hand, lower/less than and higher/greater than are associated with position. How far left and right are the numbers on the number line?

Why Math Definitions Can Be Confusing
If you're not interested in a bit of theory on how we think about definitions in math, then skip to the next section...
This issue—how less than starts to mean something different than smaller—is an example of a broader phenomenon in mathematics. A lot of ideas start out fairly intuitive and we can ground children's initial understandings of them in real or realish contexts (for example, starting to think about addition, subtraction, multiplication and division through simple story problems children can imagine and act out with blocks).
However, eventually mathematicians decide they want to extend a current definition or math concept to apply to some new situation. For a long time we could do 5 - 3, but we couldn't do 3 - 5. We had to decide how to extend subtraction to that situation (and mathematicians had debates about how to deal with negative numbers). Similarly, kids might understand division for situations like "Two kids want to share 6 blocks. How many blocks does each kid get?" and then eventually this has to be extended to situations involving fractions.
Negative numbers is one of the big places where this first happens, especially when you start to think about multiplying a negative times a negative (in addition to the book linked above, here's an interesting article on this). We want to keep some of our old rules [like the fact that a(b + c) = ab + ac] and in order to do that we end up treating negatives the way we do.
This happens throughout mathematics. There's a definition that makes sense, but then it needs to be extended to a new situation so mathematicians have to settle on a definition that will work for both the old situation and the new ones. Often the new definition is less intuitive than the old one, but it has a logic to it in terms of preserving earlier mathematical properties. This occurs, for example, when we extend arithmetic to fractions and negative numbers, in thinking about statistical properties like how consistent a data set is, and in coming up with a definition for a mathematical function (those things you graphed in high school).
This does NOT mean we need to switch away from child-centered approaches to teaching math. It means children first need opportunities to develop their more intuitive understandings. Then they need opportunities (through carefully selected problems) to figure out how they can extend these understandings to new situations. This runs opposite of a lot of traditional math teaching, which starts out by listing a bunch of definitions (which are meaningless to children if they don't have a foundation to connect them to).
Parker's Learning About Negatives
I'm not completely sure where Parker learned about negatives, but I know we've talked about them. I know we've discussed it with temperature. I also know I've asked questions about what would happen with a problem like "3 - 5." We've definitely had conversations about whether 3 + 2 = 2 + 3, and then when he said something like "it's just the same thing backwards" I asked if you do it with subtraction (i.e., does 3 - 2 = 2 - 3).
Post a Comment
What ways have you talked to kids about negative numbers?

Comments