I recently had the chance to do some math with a great group of grades 4-12 teachers from our local school district. They were taking part in a four-day professional development (PD) before the start of school. During this time they were working on Jo Boaler’s Mathematical Mindsets course, doing math, and engaging in discussion about the teaching and learning of math. I got to come in and do a short activity with them.
I’ll discuss the task we did in a minute (if you just can’t wait, skip down to “The S-Pattern Task” below), but first, I think it’s important to acknowledge how great this is. Sometimes school district PD ends up being “administrivia”—completing paperwork, aligning report cards to new standards, finalizing pacing guides, etc. I’m not saying these things aren’t valuable or that they can’t lead to deep conversations about teaching, but they are different than an opportunity to do math and reflect on teaching math. So it’s exciting to see this kind of opportunity for in-depth work at the beginning of the school year.
Going into PD “Cold” I’ve facilitated a fair amount of PD with teachers, but I wasn’t involved with this week’s work. This PD was led by Courtney Koestler, and while we had talked some about what was going on and I had done a couple of things here and there with some of these teachers in the past, I wasn’t at the PD and I didn’t know where they were in their thinking.
In this kind of situation (which also includes going into K-12 classrooms cold) it’s nice to have a task that you’re pretty sure will go well. This means it needs to stand on its own (it doesn’t require a lot of background knowledge) and it’s accessible to a wide range of thinkers. To some extent these are features to strive for in any task, but some work better than others. Part of making this work is how you frame the task, the specific questions you ask, etc., but part of it is having a good problem at the heart of your activity.
The S-Pattern Task With this in mind we picked out a pretty well-known task. We made a few changes, but basically we used the task described here, which explores this pattern:
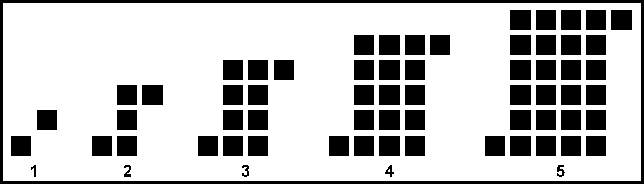
We had inch tiles available (flat, foam, 1” by 1” tiles) and most groups used them. The questions we posed are below. If you want to work on them, just get as far as you can. This task is less about “getting to the answer” than it is about exploring the pattern and describing what you find.
What patterns do you notice in the set of figures?
Sketch or make the next two figures in the sequence.
Describe a figure in the sequence that is larger than the 20th figure without drawing it.
Figure out how many squares are in the figure you chose for #3.
Explain in words how you would find the total number of tiles in any figure in the sequence.
Determine an equation for the total number of tiles in any figure in the sequence. Explain your equation and show how it relates to the visual diagram of the figures.
If you knew that a figure had 9802 tiles in it, how could you determine the figure number? Explain.
Teachers’ Amazing Thinking The teachers were great. They came up with four ways of visualizing the number of tiles in the n-th figure, shown below. They also had other strategies, like looking at how the number of tiles changed from figure to figure and looking for patterns in these numbers.
Low Floor, High Ceiling Task
We talked about how parts of this task (or similar tasks) could work for a broad range of students. Fourth graders probably aren’t going to figure out the algebraic rules, but they can think about how the pattern changes and describe how to find the number of tiles in a figure without counting by ones. This task is low floor, meaning students with a broad range of background knowledge can get started and make some progress on the task. It’s high ceiling because the mathematics can go far and push a range of students in their thinking.
This is partially due to the central problem, but it’s also partially due to how it’s framed. Look at the questions posed: There are lots of ways to be smart on this task—you can be good at looking at the figure in different ways, at describing the figures in words, at symbolic algebra, at explaining and justifying your strategy, or at identifying numerical patterns. This lets lots of kids with a variety of strengths contribute to this task.
The Challenge Moving Forward
Moving forward, teachers have to figure out how to adapt these ideas to their classrooms. This is one task. Teachers have to teach 180 days, often different courses, generally with a specific textbook as their main resource, adhering to particular standards, and in a constrained block of time (sometimes as short as 40 minutes).
But even having just spent a short time with these teachers, I’m excited about what they’re capable of and how they’ll build on all they learned this week!
Post a Comment!
A lot of people learn algebra by learning rules to manipulate symbols (like all those steps used when you “solve for x”). This task is all about building meaning for algebraic symbols. The n’s and the numbers all mean something in the teachers’ strategies.
How did you learn algebra? How do you feel about algebra?