Early Fractions
- Matt Felton-Koestler
- Aug 23, 2017
- 4 min read
A few weeks ago I wrote the following on Facebook:
Last night Parker figured out 3 ÷ 3/4 (in a story problem). This morning Parker said 12 + 5 was 15 (while keeping track of his total screen time).
Most people think of math as extremely linear. First you have to learn addition and subtraction, then you learn multiplication and division. Much later you learn fractions. People believe that math builds on itself in a very specific order, and therefore, you cannot possibly learn more "advanced" topics before more "basic" topics.
The things is, this just isn't true. Of course some problems and concepts are more advanced than others, but the landscape of how math concepts are related and the wondrous variety of ways children can navigate them is significantly more fluid than we see in many schools, textbooks, and policy documents.
The next two sections are a bit research-y. Scroll down to The Water Jug Problem if you want to skip to the fun math.
Introducing Fractions
Because my partner and I are math educators, Parker has had an extra dose of math conversations from a young age, but the kinds of conversations we have are ones that almost all children are capable of, because they build on familiar, everyday experiences.
Most children have experiences sharing things, and this is how fractions should first be introduced, with problems like "There are 2 kids. They are sharing 3 brownies. (If they eat all the brownies and they each get the same amount,) how much does each kid get?"
It turns out young (kindergarten age) children can solve problems like this. They won't write "1 ½", but they will be able to either draw a picture showing how much each kid gets or say something like "one brownie and a half a brownie" or "one brownie and a piece." Empson and Levi's book, Extending Children's Mathematics is an excellent guide for how to start with children's natural strategies for thinking about simple fractions and build towards more sophisticated understandings. Note: it's actually really important to use full words like halves and fourths for quite awhile and only introduce the formal notation (like ½ and ¼) later—the formal notation tends to confuse students and make them think of two different numbers (a "1" and a "2") instead of a single quantity (a half).
Long story short (ha!), we've done a number of problems like this with Parker, and Parker seems to have a pretty good understanding of what a half is and sometimes seems to understand fourths and thirds. So I thought it would be fun to try out a harder problem.
Dividing Fractions
Before getting to the problem, though, let's return to the myth that math has to be taught in a particular order: most people think addition and subtraction are easier than multiplication and division. First, this isn't even true all the time with whole numbers (certain multiplication and division situations are far easier than certain addition and subtraction situations for young kids). Second, it's pretty much flat out backwards for fractions. The brownies problem above is typically thought of as a division situation and that type of problem is the go to for introducing fractions.
Plus, these problems are great for thinking about equivalent fractions—answers to the brownie problems include "3 halves" and "1 and 1 half". These are two different names for the same amount. With a problem like "4 kids share 6 brownies" you get even more equivalent fractions (how many answers can you come up with for this problem?). This lays the foundation for understanding common denominators because kids will know multiple names for the same fraction instead of having to blindly follow an algorithm. Later, children can solve more challenging fraction division problems that will naturally bring in common denominators. If you do this ground work first, adding and subtracting fractions is much less challenging.
The Water Jug Problem
Take a minute to solve this problem—I encourage the use of a picture.
You are going on a long hike. You have 3 jugs of water. Each day you need to drink 3 fourths of a jug of water. How many days can you hike before you have to refill?
Below is Parker's picture. It's a bit messy, so I made a cleaner version of it. At first Parker had just drawn the three jugs, cut them into fourths, and was pointing while explaining. I suggested shading in and then later drawing the lines for clarity. This wasn't simple for Parker—there were a couple of false starts, especially when Parker was trying to do the whole thing mentally, but Parker got it. And more importantly, Parker understood it.
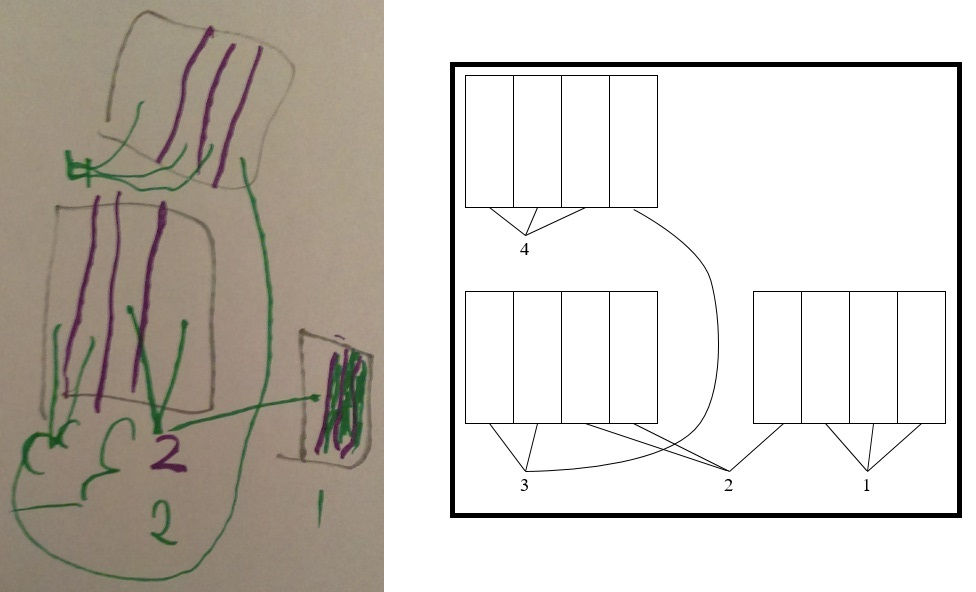
The Myth of Linear Math
The next morning Parker gave an incorrect answer to a question about how many minutes of screen time P had used up already (12 minutes on one video and 5 on another).
Because of the myth that math learning must proceed in a particular order, too many kids who have not "mastered" one skill (like whole number addition) are often denied the chance to think about other "harder" math (like fractions).
Even worse is that along with the myth that some topics must come first, is the idea that "basic facts" and memorization must come before more advanced skills like solving new problems and inventing strategies. Nothing could be further from the truth—the last several decades of research have consistently shown that children best learn mathematics by inventing their own strategies to problems (just like Parker did on this problem).
This is a waste. It damages children because it turns them off of math by denying them the chance to think. Young children like math because they like challenging problems, but after a few years of having to memorize basic facts before they can do anything interesting they get turned off of math and, worse yet, they learn not to think.
Next Time
I talk about how Parker did with the follow up problem: "Same basic situation: You drink 3 fourths of a jug a day, but this time you have 4 jugs. How long can you hike before filling up?"
Further Reflection (leave a comment!)
How did you think about the water jug problem?
Fractions are where we start to lose a lot of kids in math (in part because it starts to become too complicated to just fake it with memorization)—how do you feel about fractions today?

Comments