Tiling, Area, and Time to Explore
- Matt Felton-Koestler
- Aug 12, 2017
- 5 min read
Disclaimer: This post is a little long and a little "researchy," but I hope it's still accessible. If that's not your cup of tea then check out the next post.
Last time I talked about renaming numbers while reading A Remainder of One. I had started to get out blocks to do more with Parker, but P's interest was waning. As I got out the blocks (actually Duplo LEGOs) I thought of another type of problem and P was game after hearing it was from a research article (it is possible I sometimes inflate Parker's ego to get P to do more math with me).
The problem is to figure out how many blocks will fit if we try to fill in the entire rectangle below. Notice I only drew some of the block outlines—P had to fill in the rest mentally. Because I wanted to recreate the research article with my own kid (that's how I get my kicks) P wasn't allowed to use any blocks and couldn't draw on the paper.

Rectangle 1
I don't recall the details of P's strategy on this one, but I think P got it before drawing in the blocks. I was really interested to see how P would draw in the blocks—basically I wanted to know what P sees in this rectangle. Let's look at examples of things some of the kids did in the article.
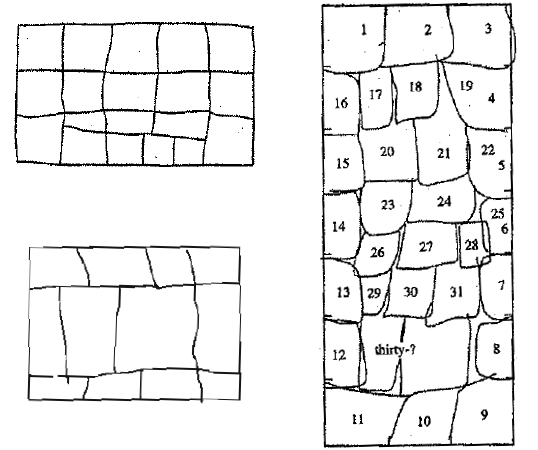
Some children's drawings on similar problems
Kids thinking is amazing and fascinating!!
As adults we may take for granted the idea that there "is" an array of neatly ordered squares that we can break this rectangle down into. But that array isn't really there. Our mind puts it there (it fits because of the properties of the rectangle, but that doesn't change the fact that our mind puts it there). In a very real way these kids see a different rectangle—for them there is no array.
Learning to see the array is developmental, meaning there are a series of steps/stages kids go through as they get closer and closer to seeing the array. This developmental process is not age dependent; instead it depends on their experiences (their formal and informal learning opportunities).

Parker filled in the rectangle with an array. So what kinds of experiences has P had to get to this point? I can think of two big things. First, we play with LEGOs a lot (Duplo and regular). I often refer to pieces by their dimensions and have talked about what I mean when I ask for a "blue 2 by 3" so P can help me look. Second, Parker plays a fair amount of Minecraft (I think this is a pretty good game, but I may have introduced it a bit early, because P is obsessed). If you don't know, Minecraft is a world made up of cubic blocks—you can dig (mine) blocks up, place new blocks to make structures, etc. Parker also watches videos of people playing Minecraft and building things and they'll often include directions like "make a five by seven frame". So I think P has had a lot of opportunities to begin to see 2D space in a grid.
Still room to grow
Parker's thinking on the second rectangle was a little different. I don't have a before shot for this one, but you may be able to tell that I didn't draw in full squares along the top and side—I just drew hash marks like on a ruler. Before drawing, Parker thought there would be 8 squares on the top and bottom and then two on either side (so 8 + 8 + 2 + 2). Then Parker drew the lines and counted by ones. We compared with the previous strategy and Parker figured out P had not counted the middle squares. So while Parker is beginning to see the array, it's not 100% there all the time, and Parker certainly couldn't say, "oh it's a 4 by 8 rectangle, so there must be 32." This is what I mean when I say learning to see the array is a developmental process—there are a series of steps that start with something like the pictures from the article and end with something like "oh it's 4 by 8 so...". Parker is somewhere in the middle of that process.

Rectangle 2
Ignore the double line on the bottom—I had to fix the rectangle (give me a break I just had LEGOs and a marker)
Interesting, I guess, but so what?
The idea that adults and children quite literally experience different worlds is hugely important to child-centered mathematics. This means that if I try to speak "adult" or "mathematician" to a child it will almost be like we are speaking different languages. They can memorize proper responses and parrot things back, but they won't understand what they are saying and won't really learn the language unless I provide them with the right kinds of experiences. (Also, the longer I force them to just parrot back responses the harder it gets for them to recover and really figure out what's happening.)
In this case, these problems demonstrate how detrimental it can be to force kids to use a formula like Area = length × width before they are ready. Look at the children's drawings from the article. Those kids simply cannot (yet!) make meaningful use of this formula or understand why it makes sense. Instead, children need lots of opportunities to fill the space of rectangles (and, perhaps more importantly, irregular shapes) with square tiles and other manipulatives so they can build an understanding of what area is before being taught (or better yet, asked to derive) formulas. If the shapes are challenging and there are a variety of tools available (think tiles, tracing paper, circular discs, grid paper), then a broad range of learners can be challenged.
If you accept the premise that children and adults experience different worlds, then it becomes much easier to refocus math teaching on children's ways of thinking and slowly guiding them towards mathematicians' ways of thinking. Doing this means you have to pose problems, allow children to develop their own approaches to these problems, listen to how they think, orchestrate conversations between them so they confront different perspectives, and carefully consider how to question them and what problems to give next to move the class forward.
This is hard work! It requires a lot more from teachers than getting up and lecturing. They need to know the math they are teaching deeply and flexibly. Elementary math may seem basic, but navigating all the ins and outs, especially when you open it up to children's thinking, is complicated (I still learn new ways of looking at these ideas).
Unfortunately, we don't give teachers the support they need to do this. They didn't learn this way in school and they have few opportunities to learn it on the job. Teachers need long-term professional development focused on how these ideas work in their classrooms. Investing in mathematics coaches, providing common planning time, allowing teachers time to work with these ideas over years, and giving them the freedom to adapt their curriculum based on what they are learning are all crucial to building their capacity to do this kind of teaching.
Next time
Next time is a short post about a card game we used to play that is good for building some early number sense.
Further reading
If you're interested in the article featured here, the citation is:
Battista, M. T., Clements, D. H., Arnoff, J., Battista, K., & Borrow, C. V. A. (1998). Students’ spatial structuring of 2D arrays of squares. Journal for Research in Mathematics Education, 29(5), 503–532.
Here's a link to the source (if you'd like to know how to get a copy, email me):
Question (post a comment!)
What do you remember about learning area? If you work with kids, what have you noticed about their thinking? Have you seen examples of kids exploring area with their own strategies?

Comments